How to Calculate the Chances of a Pokémon Trainer Winning a Battle - Using Entropy to Measure Variety
7 min read
People can become bored with the same options. Variety keeps the experiences fresh and exciting, may it be when shopping or going out for food or drinks. However, variety is a very subjective concept. How does a business know whether they are offering a good variety of options? How can they assess whether their variety is improving? Entropy, used in information theory to measure “uncertainty", can be a good mathematical solution.
Here’s an interesting challenge for me: Is it easier to explain a mathematical method or Pokémon? Let’s find out - and please give feedback if I failed miserably at both.
Disclaimer for pokémon fans: I’m mostly referring to the first generation in this post, especially from the gameboy games.
Pokémon - Gotta Catch ‘Em All
Pokémon are animal-like creatures - with superpowers. People can catch them and use them to fight other pokémon - by playing the Game Boy game. Actually that sounds cruel, but hey, it’s meant for kids, so it’s all made in a very cute and fun way *yey*. Still, why would people want pokémon to fight each other?
To train their own pokémon and make them stronger.
To catch the other pokémon.
To battle with another pokémon trainer.

A trainer is allowed to carry with them up to 6 pokémon. So if a trainer has caught more, they need to be strategic with their selection.
Pokémon are categorised by types: normal, fire, water, electric, grass, ice, fighting, poison, ground, flying, psychic, bug, rock, ghost, dragon, steel, fairy.

There are even pokémon with a combination of types.

Some types have a natural advantage over others, i.e. they are stronger.
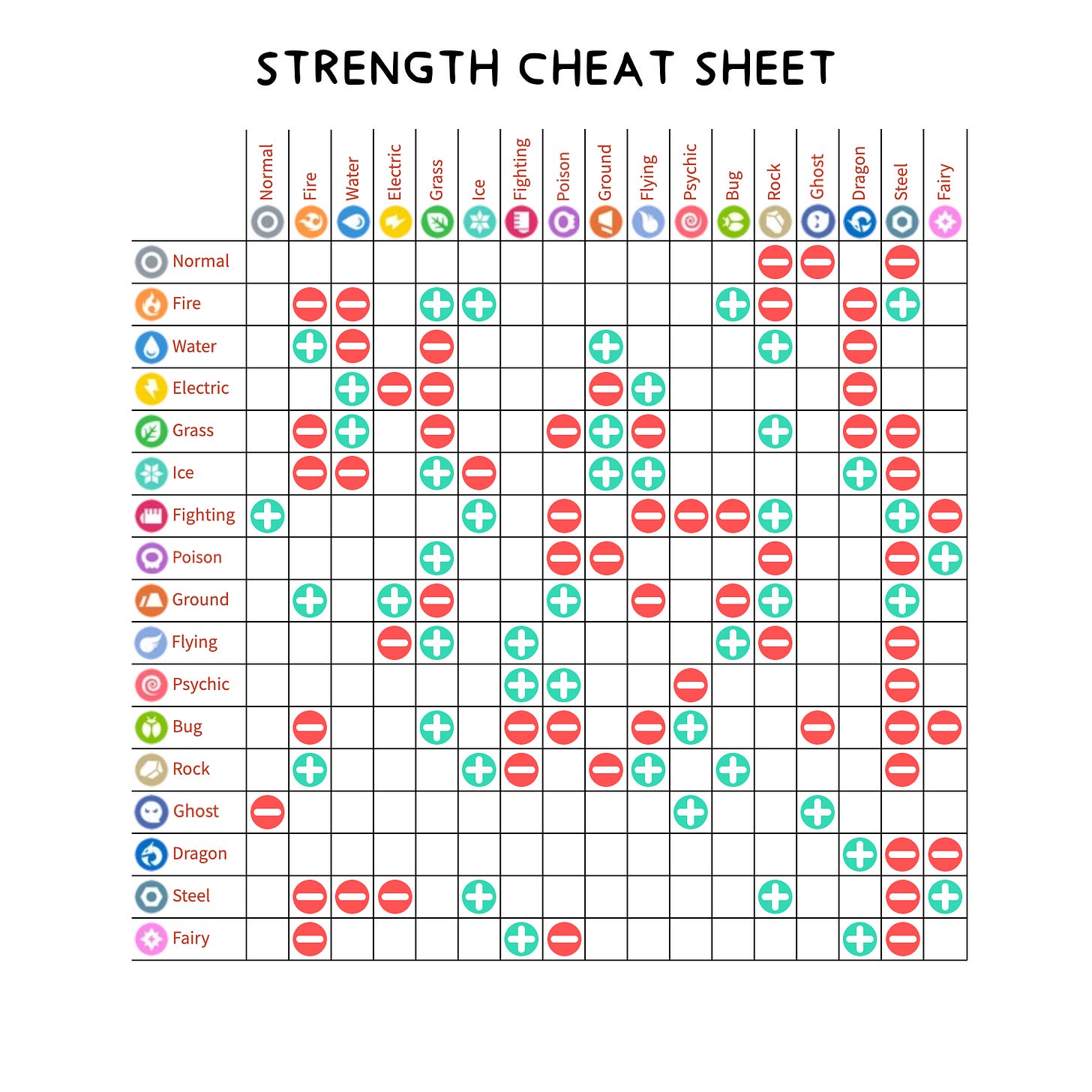
What’s Your Type?
Some trainers like to specialise on certain types - they make their entire personality about it. For example Misty loves water pokémon and Brock prefers rock pokémon.

But is that really a smart strategy if you want to win a battle?
If I were a pokémon trainer - and yes, I played the Game Boy game multiple times, even as an adult -, I would just catch and train one strong plant pokémon to defeat both of them. Easy peasy.
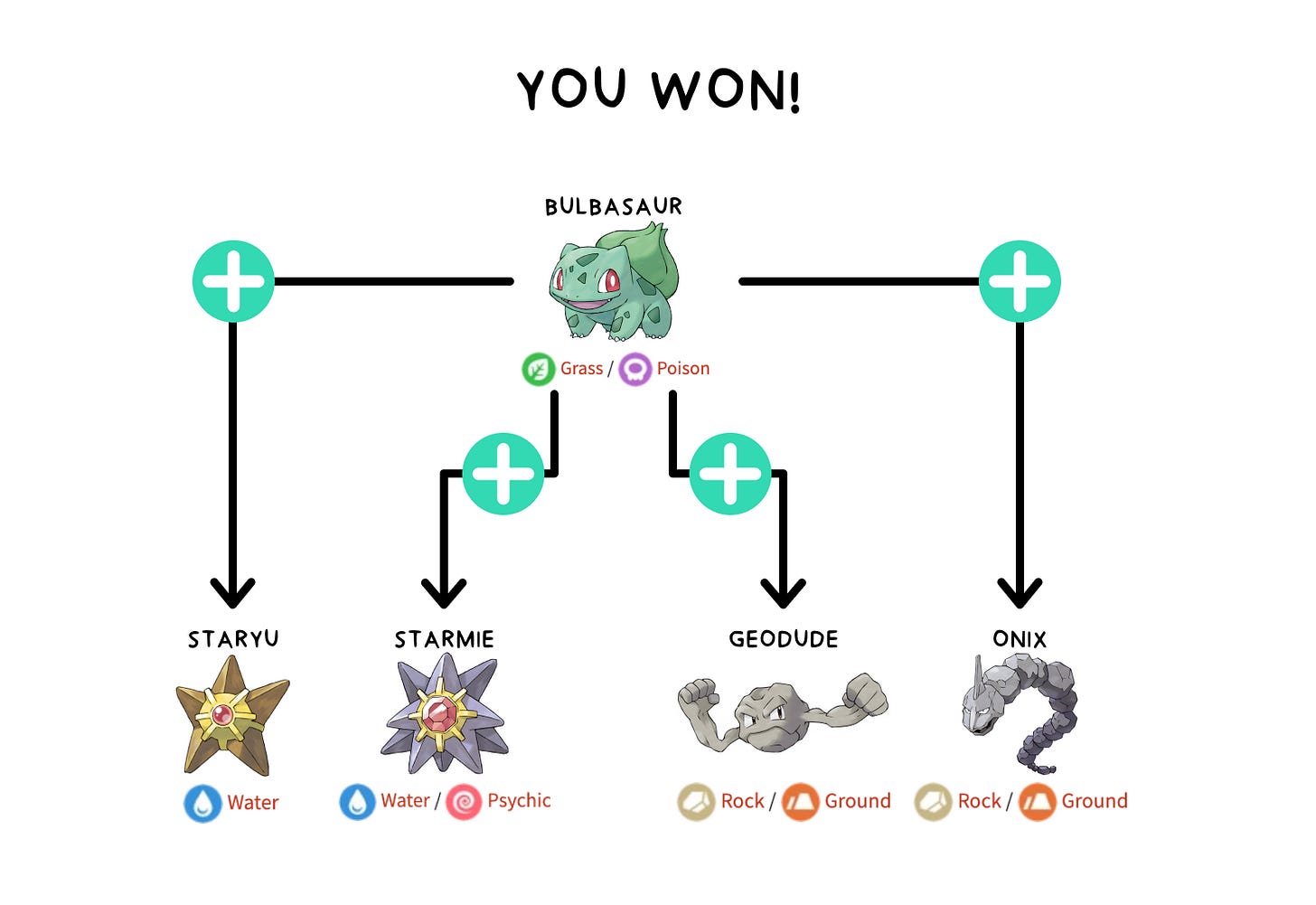
It’s easy to determine the chances of winning when knowing the trainer’s preferences or even pokémon in advance. How about evaluating a strategy in general?
Be Prepared
In the Pokémon League, the championship, a trainer is not able to switch pokémon between battles. So they need to be prepared for any opponent. The best way to do that is to ensure a high variety of types among the 6 pokémon.
Let’s consider 7 trainers as the opponents in the championship.
Variety can be quite subjective and is usually determined by examining a selection of options visually. Just by looking at the different pokémon sets, one can decide for themself the grade of variety. My examples range from no variety to perfect variety, and even super perfect variety - kinda like evolution levels.
A simple way to quantify the variety for each trainer is… simply counting the number of types in the setup. Job done!
This analogy here is just a simple example, too simple to apply this solution to more complex problems. So we look at a more sophisticated approach: entropy.
Instead of just counting the types, we represent the occurence of types in a set as a share. For example if there are only pokémon with exactly 1 type and only 1 of them is of type water, then the share of type water is 1/6. If one of the pokémon is a combi of 2 types, like water & ice, and there is no other water pokémon, then the share of type water is 1/7.
A small example first to not get overwhelmed.
This is what it looks like for all 7 trainers and the different types.
The specialty about entropy is that it uses the negative logarithm as a weight. Before I explain further, let’s look at the shares again and compare them with their negative logarithm.
As can be seen, the negative logarithm is getting closer to 0 when the share is getting closer to 1 (when the share is increasing). On the other side, it’s increasing a lot when the share is getting closer to 0 (when the share is decreasing) - the limit of the negative logarithm is actually infinity, meaning there is no limit.
What to do with this information now? Similar to a weighted average, we can now sum up all the shares combined with their negative logarithms as weights and get a single number for the entire set of pokémon - this is the entropy.
The value is lowest for the trainers with a low variety of types, and highest for the trainers with a high variety.
Is It Really Worth the Effort?
Is entropy actually more suitable than other more well-known and simpler measures? What about using the mean or weighted mean? Let’s compare entropy with more well-known measures:
count of unique types: as already seen, this is simply counting the number of unique types, ignoring how often each one occurs
mean: the arithmetic mean of the shares
median: the median of the shares, i.e. the middle value when ordering all shares in ascending order
weighted mean: the arithmetic mean of the shares weighted by how often each one occurs
As baseline we start with no variety. Whenever the visually perceived variety of the pokémon set increases, the values of the measures should reflect that:
Whenever the value of the measure is changing as expected, it’s coloured in green, otherwise in red. No change is considered as “not as expected”, so it’s red too.
As can be seen in the visualisation, entropy is the only measure which is always behaving as expected. It is the most sensitive to changes in variety.
Without having to know a trainer’s specialty, we can use this value now to evaluate their chances of winning multiple battles against different trainers and their different pokémon with the same set of pokémon. The higher the entropy, the higher the chances of winning.
Have you played Pokémon on the Game Boy? If yes, what was your preferred strategy?
Hi, I'm Nadine. I empower people through comprehensive training and coaching in data analysis and mathematical modeling, equipping them with the tools and knowledge to excel professionally. If you’re interested in finding out how I can support you in your learning journey, book a free 30-minutes introduction call with me right here, send an email to nadine@mathemalytics.com, or connect with me on LinkedIn.














I enjoyed that!